Ecuación de la cuerda vibrante
Supongamos una cuerda de longitud l sujeta por los extremos A y B que vibra en el plano OZX
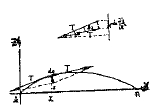
Vamos a razonar las matemáticas de este problema físico utilizando la guía o la imagen de una guitarra eléctrica. Así pues la cuerda vibrante AB podría ser una de las 6 cuerdas de una guitarra eléctrica que, tirando de ella y soltándola, empieza a vibrar emitiendo un acorde, esto es un sonido.
Nos plantemos saber la ecuación del movimiento de esa cuerda cuando está vibrando en el espacio y el tiempo. Dicha ecuación del movimiento la llamaremos:
z(x,t)
Llamaremos T a la tensión de la cuerda, una constante física que depende del material y la geometría de la cuerda.
Llamaremos ρ a la densidad lineal del material de la cuerda. Como ambas son constantes positivas, podemos definir:
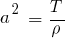
Haciendo razonamientos de tipo físico y utilizando las leyes de Newton, llegamos a plantear la ecuación diferencial de la cuerda vibrante:
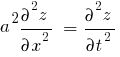
Como vemos es una ecuación diferencial de segundo orden en derivadas parciales. No necesitamos entrar en cómo se resuelven estas ecuaciones. Lo que pretendo explicar es otra cosa, pero si diremos un detalle importante sobre las soluciones de esta ecuación diferencial. Recordemos que la incógnita de esta ecuación diferencial es precisamente la ecuación del movimiento de la cuerda vibrante, que es justo lo que pretendo hallar: z(x,t)
- Solución general de d’Alembert → Sin interés para los fenómenos físicos de la acústica. Es la solución mas general.
- Solución particular de Bernouilli → Construida para que las matemáticas desvelen las leyes de la acústica.
La solución de Bernouilli, sería:
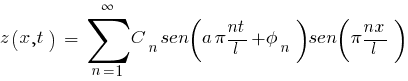
donde las amplitudes serían:
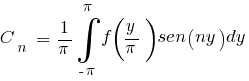
Con lo cual la solución particular de Bernouilli completa y desplegada toma la forma:
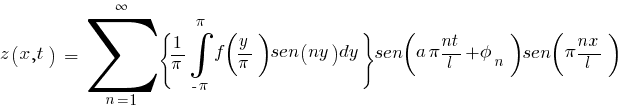
Donde y es una variable muda de integración.
Esto es una suma infinita de funciones. Pero fijaros que el hecho de que sean una suma infinita de funciones nos da las leyes de la acústica:
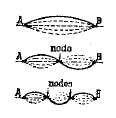
El primer sumando es el llamado tono fundamental
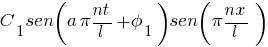
Al segundo sumando se le llama primer armónico con frecuencia doble y un nodo:
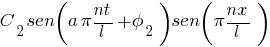
Al tercer sumando se le llama segundo armónico con frecuencia triple y dos nodos intermedios
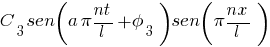
Para calcular las amplitudes Cn, se usa lo que se llama un desarrollo en serie de Fourier. Históricamente hubo controversia sobre si cualquier función se puede desarrollar en desarrollo en serie trigonométrica o de fourier. El mismo Fourier demostró que si eran posibles tales desarrollos.
Aplicación al caso de la guitarra eléctrica
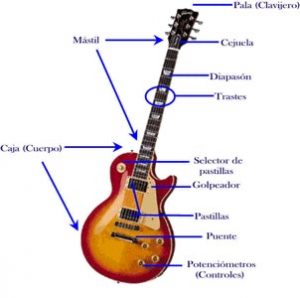
Veamos como salen las leyes de la acústica atendiendo al ejemplo de la guitarra eléctrica:
- Cada una de la 6 cuerdas que tiene una guitarra eléctrica es de un grosor diferente, luego aquí estamos variando ρ , por eso a igualdad de longitud, cada cuerda suena diferente.
- Con los trastes lo que hacemos es acortar la longitud l del segmento AB, es decir, variamos l.
- Cuando tiramos con la púa con mas o ménos fuerza de una cuerda, estamos actuando sobre la tensión T.
- Observar que los 3 parámetros fundamentales de la ecuación: ρ, T, l están presentes en la solución: z(x,t), por lo tanto todo instrumento de cuerda tiene que poder variar estos parámetros para generar toda la gama de sonidos posibles.
- Cuando pulsamos una de las 6 cuerdas (ρ) en un traste determinado (l) con una fuerza determinada (T) → estoy produciendo un sonido de una frecuencia determinada (Hz).
Supongamos que la nota obtenida sea do. Entonces, el primer armónico da la octava del tono fundamental.
Se define octava como el intervalo de frecuencias, es un intervalo cerrado de números reales, entre una frecuencia dada y su duplo.
No todas las octavas son audibles por el oído humano. El oído humano solo oye entre 20 y 20.000 Hz. Las octavas que se pueden oír son 10
Los sucesivos armónicos dan las relaciones de frecuencias de los intervalos musicales puros:
armónico 1 → octava 2/1
armónico 2 → quinta 3/2
armónico 3 → cuarta 4/3
armónico 4 → tercera mayor 5/4
armónico 5 → tercera menor 6/5
armónico 6 → segunda 7/6