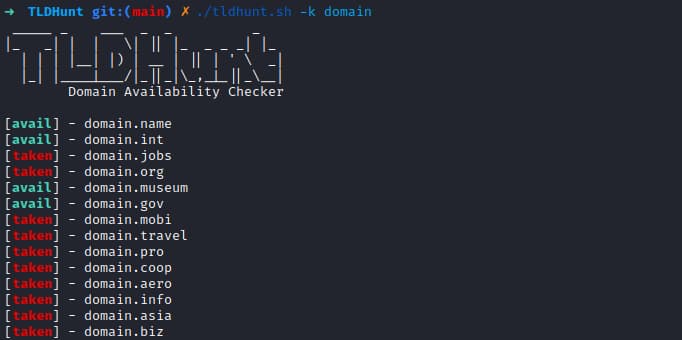
El Misterioso grabado de Durero: Melancolía

En lo alto está el rostro de Diana en Quíos, que parece triste a los que entran en el templo, alegre a los que salen. Incluso la carta de Pitágoras, ejecutada con una línea bicorne, ofrece un excelente final a quienes muestran el aspecto sombrío del camino correcto. De las sombras, que surgieron de la profunda oscuridad, al fin serían bienvenidas, ahora más duras
Imagen: Alberto Durero: Melencolia I, 1514 – Staatliche Kunsthalle, Karlsruhe
«Melancolía» es uno de los cuatro estados de ánimo. Es el menos deseable porque conduce a la depresión, la apatía e incluso la locura. Sin embargo, la ventaja de ser melancólico era que este estado de ánimo tiende a asociarse con los individuos más creativos e inteligentes. Se creía que carpinteros, matemáticos, artistas y gramáticos tendían a ser melancólicos. El murciélago es el símbolo de la eternidad. Signo de Saturno, el dios afiliado a la melancolía. La obra representa simbólicamente, en términos alquímicos, las dificultades encontradas en el intento de transformar el plomo (almas de las tinieblas) en oro (almas que brillan). Según la tradición astrológica, la esfera alquímica estaba dominada por el planeta Saturno y estaba ligada al sentimiento de melancolía. Otros elementos que despiertan esta emoción son el arcoíris y el cometa. Las llaves representan el conocimiento, capaz de liberar al hombre de su estado melancólico. Otro símbolo de esperanza es el murciélago que se ilumina con la luz que barre la oscuridad.
El cuadrado mágico
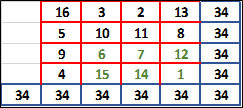
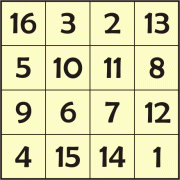
El cuadrado mágico contenido en la obra es muy complejo. De hecho, no es solo la suma de los números de las líneas horizontales, verticales y oblicuas lo que da 34, sino también la suma de los números de los cuatro sectores cuadrados en que se puede dividir el cuadrado y también los cuatro números en el centro, si se suman dan 34. Además de los cuatro números en las esquinas. Además, si toma un número en las esquinas y lo agrega al número opuesto, obtiene 17, en cambio, si toma un número del centro y lo agrega a su número en la parte inferior derecha (o superior), siempre obtiene 17.
Además, si se toman los números centrales de la última línea encontrarás el número 1514, el año en que se creó la obra y el año de la muerte de la madre de Durero.
Planteamiento del problema
Si hemos leído atentamente las características del cuadrado mágico de Durero, vemos que se puede plantear un sistema de ecuaciones lineales, para tratar de dar con todos los cuadrados mágicos de Durero que existan.
El sistema es el siguiente:
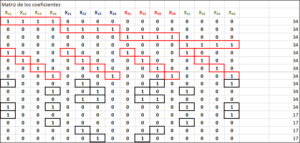
Como vemos es un sistema de 16 ecuaciones con 16 incógnitas. Lo analizamos por el teorema de Rouché-Frobenius y hallamos que es compatible indeterminado, o sea que tiene infinitas soluciones. Habría pues infinitos cuadrados mágicos de tipo Durero.
De hecho el problema tiene 6 grados de libertad. Se pueden variar los coeficientes de esos grados de libertad en el Excel que he creado a propósito. Simplemente cambiando las cifras en verde. Dicha hoja se puede descargar aquí.
La Solución general del sistema sería:

Y el desarrollo completo de la solución se puede encontrar aquí.
Para resolver los tediosos cálculos de un sistema de 16 ecuaciones con 16 incógnitas, no he encontrado mejor solución que esta excelente página:
https://matrixcalc.org/es/