Resolución de Ecuaciones Cuárticas

Introducción

Este es un problema que está resuelto desde la Edad Media. Además en internet hay infinitas páginas que abordan el problema. Entonces ¿por qué hago esta hoja de cálculo que lo resuelve?. Pues porque en primer lugar yo no he visto que exista nada parecido. Ademán las «infinitas» webs que abordan el problema, es verdad que lo abordan pero no dan una solución satisfactoria.

Errores, fórmulas que no funcionan, métodos poco prácticos, etc. Por no hablar de la IA varias a las que he preguntado y han fallado como escopeta de feria. Sencillamente las fórmulas que daban no funcionaban eran fakes. Mucho cuidado con las inteligencias artificiales sobre todo en temas matemáticos y de fórmulas. No dan una.

Así que he recurrido a la Wikipedia para sacar la fórmula, que si funciona, y he construido la hoja de cálculo que se puede descargar aquí y que es completamente operativa aunque tengo que pulirle algún detalle.

Todo esto surge no por casualidad sino como parte de un proyecto mayor relacionado con las espirales de Kozyrev, que ya veremos si algún día acabo. Es francamente complejo.

Resolución de Ecuaciones Cuárticas

Sea la ecuación cuártica:

Reducimos a la forma mónica:

Donde:

Y la ecuación cúbica resolvente sería:

Que puede ser resuelta por el método de Cardano:

Pues veamos como se resuelve una ecuación de tercer grado:

Dada la ecuación cúbica:

Se calculan las siguientes cantidades:

Con base en los valores calculados de Q y de R, se calcula la Discriminante, que definirá las posibles soluciones de la ecuación:

Al ser D, la discriminante, se tiene:

1. i) Si D>0 entonces una de las raíces es real y dos de ellas son complejas.
2. ii) Si D=0 entonces todas las raíces son reales y al menos dos son iguales.

iii) Si D<0 entonces todas las raíces son reales y distintas.

Para el caso i)

Calcular:

La primera raíz real se pueden calcular simplemente como:

Las dos raíces imaginarias se pueden calcular de la siguiente manera:

Para los casos ii) y iii)

El cálculo de las tres raíces reales se simplifica un poco si se reescriben las soluciones mediante las siguientes fórmulas trigonométricas:

donde:

En el caso ii) , dos de las tres raíces calculadas, serán iguales.

Bueno, pues con todo esto creamos una hoja de cálculo para resolver las ecuaciones de tercer grado:

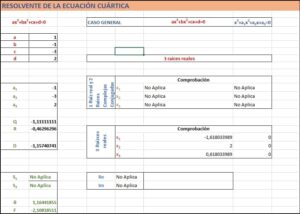
Ahora continuemos con la resolución de la ecuación cuártica:

Volvemos a la ecuación resolvente:

Sea y una raíz real positiva o negativa, eso da igual. Entonces calculamos los siguientes valores:

Y las 4 soluciones serían:

La ecuación resolvente de tercer grado puede tener 1 o 3 raíces reales. ¿Cuál usaremos como valor de y para los cálculos auxiliares de la ecuación de cuarto grado?.

Pues aquella que haga positivo y por lo tanto real el valor de m que aparec e en los cálculos. Eso lo hace todo automáticamente la hoja de cálculo que he hecho.

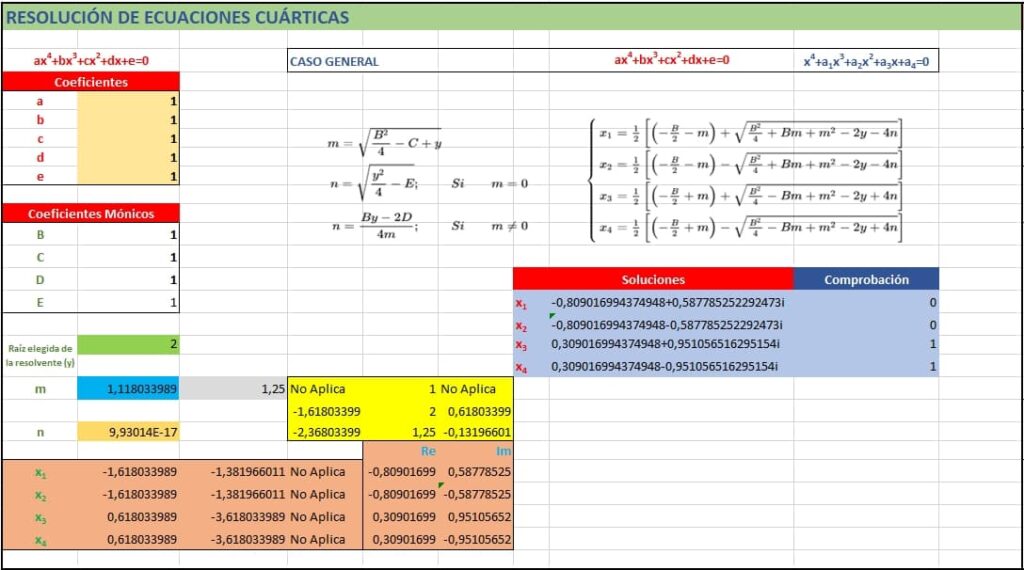
La soluciones de la ecuación de cuarto grado serían:

• Si la ecuación cúbica resolvente tiene una raíz real, la ecuación cuártica tendrá dos soluciones reales y dos soluciones complejas conjugadas.
• 2) Si la ecuación cúbica resolvente tiene dos o tres raíces reales, la ecuación cuártica tendrá cuatro soluciones de manera aleatoria definidas así:
  • a) Cuatro soluciones reales distintas.
  • b) Dos pares de soluciones complejas conjugadas.
  • c) Dos raíces reales dobles.
  • d) Una raíz real simple y una raíz real triple.
  • e) Una raíz real cuádruple.
  • f) Una raíz real doble y dos soluciones complejas conjugadas.
  • g) Dos raíces complejas conjugadas dobles.
  • h) Una raíz real doble y dos raíces reales simples

La hoja también es capaz de operar con números complejos y de comprobar que las soluciones halladas verifican la ecuación.

La forma de usar la hoja de cálculo es introducir los coeficientes de la ecuación: a,b,c,d,e en la zona marcada en color arena. Las soluciones van marcadas en la zona azul. No hay que introducir datos en ninguna otra zona. Solo con los coeficientes se calcula todo.